Eldritch Noodle's Mathematical Tier List

In every competitive asymmetric game players often argue about what characters or factions are “the best”. Now, there is no right answer; that’s why it’s a fun topic to argue. Because each faction is different, every matchup is unique. Even the strongest faction may simply be bad against a much weaker one.

With this in mind, I set out to use the data the Summoner Wars community has collected to build a ranking of all of the factions. Everyone loves a good tier list!

Luckily for us, we’ve a pretty good set of data from the SW league matches. Since every matchup between two factions is played in pairs with each player playing both factions, the overall faction win rate should be fairly independent from player skill. This isn’t perfect, since players are likely to be better or worse playing different factions, but it’s about as good as we can reasonably ask for from a small dataset. From now on we’ll forget about the individual players, and just think in terms of matchups: over 56 games of Cave Goblins vs Phoenix Elves, Cave Goblins won 46% of the time.

My first attempt was to use the well known Elo ranking system, treating each faction as a player to be ranked. If you’ve never heard of Elo it’s the standard system used to rank competitive chess players and variations of it are used for most ranked video games. If you queue up in Hearthstone, MTGA or League of Legends it’s likely something very similar to Elo is being used to find players of similar skill.

Elo, however, has its trade offs. The big selling point is each player’s score can be updated after a match without knowing anything about anyone else. This makes it useable across many tournaments where different players enter. However, the score is dependent on the order of games played. This can actually be a good thing for player ranking as people’s scores often improve with time. However, when it comes to this project it presents a problem: if Phoenix Elves won the first 26 games and then Cave Goblins the last 30, you get a very different score than the reverse. What you can do is randomize everything. Randomize the order of all games across the league and then average the result over a thousand tries. This works, and notably has a similar result to my ultimate approach, but isn’t quite right.

You see, Elo is a probabilistic model. It is designed so that if you know two players’ scores, you can predict the probability one player will win. For us, the outcome of Phoenix Elves vs Polar Dwarves isn’t that dependent on our first matchup (CG vs PE). The math of Elo tells you that over the long run it should approach the right answer, but since our use case doesn’t fit its assumptions, it’s guarantees don’t actually work.

But luckily there’s a better way! What we want is not a probabilistic model, but simply a ranking. Basically, over the specific games played in the league, who’d score the most “points” if you took into account the strengths of your opponents? But hold on a moment, you say, all this maths seems a little much. Can’t we just look at the win rate of each faction? Well you could, but given the data we have, it wouldn’t be very good. Win rate depends a lot of the matchup. Wins against a weaker faction really shouldn’t count the same as wins against a stronger one.

Luckily there’s already a good solution to this same problem in a different setting: College (American) football. Now I’m not an expert on the subject, but I’ve been told that each school team plays against only a small subset of the total field, teams very significantly in strength and not everyone plays the same number of games. Now luckily for us, there’s a pretty clever mathematical proposal that uses a little bit of linear algebra to solve this problem [1] and applies perfectly to our Summoner Wars tier list goal. The basic idea is: each faction’s score should be a sum of it’s win-rates weighted by the (final) scores of the other factions it has played against. The computer solves this system of equations and, voila, you get your scores.

The Results

Enough with the damn maths, you say! I’ve already scrolled past this to the graphs and you can’t stop me. Hah-haha. Ok, ok, but if you’re confused about what the ranking is, just think of it as a point score each faction gets based on its victories. All the points are neatly weighted off each other so that winning against a stronger team is worth more. The number alone doesn’t really “mean” anything, they’re just important in context that one is bigger than another. Also it’s dependent on the matchups played in the league. Just because Polar Dwarves is ranked higher than Cave Goblins doesn’t mean it will actually do better in that specific matchup.

Now without further ado, the ranking of factions from the league:

Boooo! No error bars, the people yell, I want my tier lists absolute with no wiggle room! I shall wield The Big Data to crush any forum poster who dares to claim Fallen Kingdom is good, scoff.

Err well, um. Moving on… The error bars are drawn from the margins of error in the games played in the league. Since the league isn’t all that big, we can’t claim with too much certainty that CG vs PE really is a 46% win rate, only that it’s close-ish. So it’s indeed possible that Fallen Kingdom’s true rating is actually at the top of its black error bar and one of the best, while the other factions are a little lower. The odds are about the same as missing with 3 ranged dice so… Well you get the picture.

Now, you shouldn’t believe me just because I have some pretty graphs. But I do have one pretty graph that I’m pretty sure will be pretty convincing. Let’s see if the faction strengths mean anything about actual matchups?

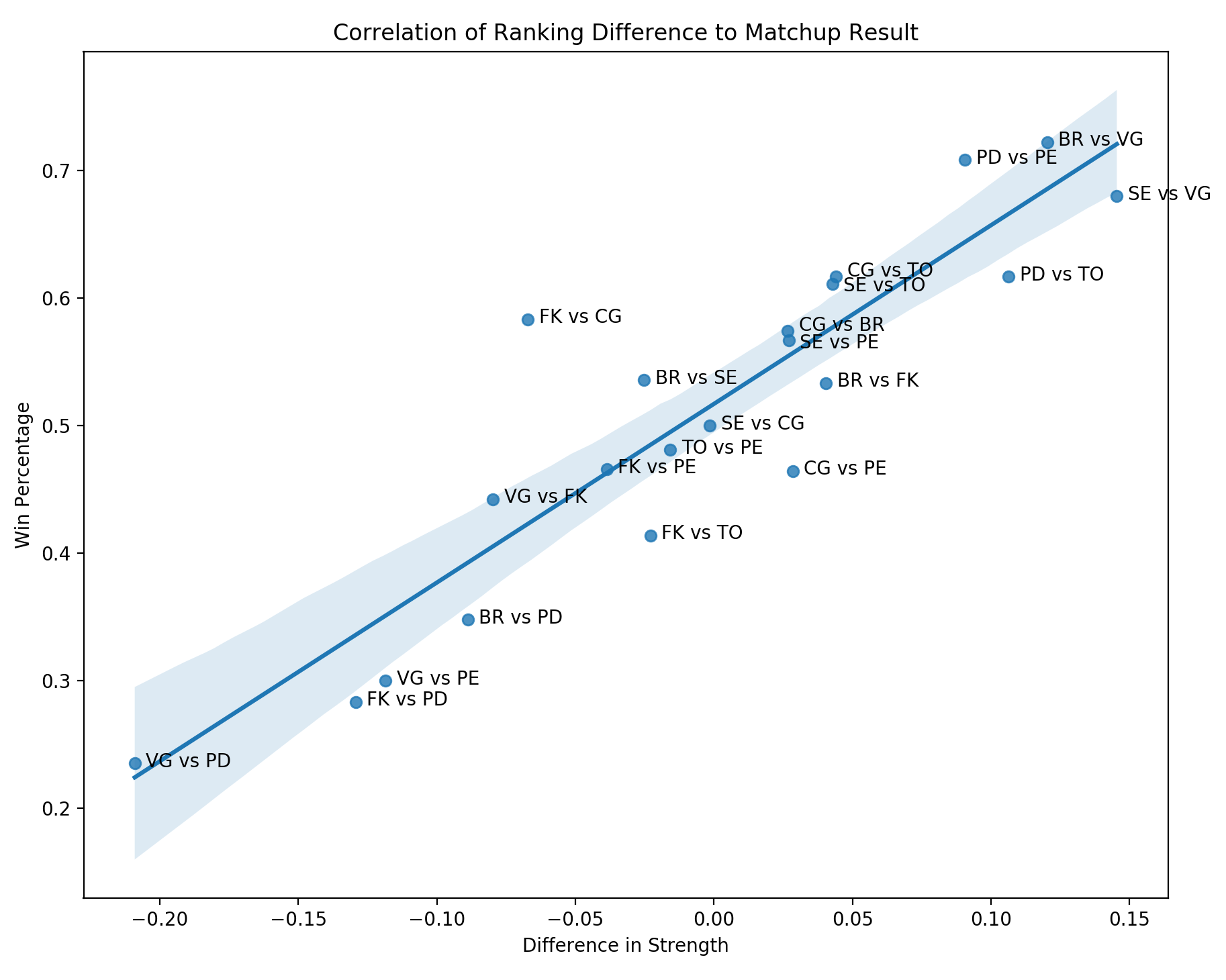
What we see here is the correlation between the difference in scores of two factions and the result of their matchup in the league. What we see is that overall, most matchups are fairly close to the trend line. However, there are still a number of outliners, especially when it comes to factions fairly close in strength. We’ll have to see if this holds up in the future.

First Turn Advantage

But wait! There’s more! The league also has data on who went first in each game. Because of this we can attempt to answer the age old question of how important is going first. To do so, we’ll break each faction into two: the version where it always goes first and the one where it always goes second. Note that PE going first only ever plays factions that go second. However, since there’s enough interlinking games we can still perform our ranking.

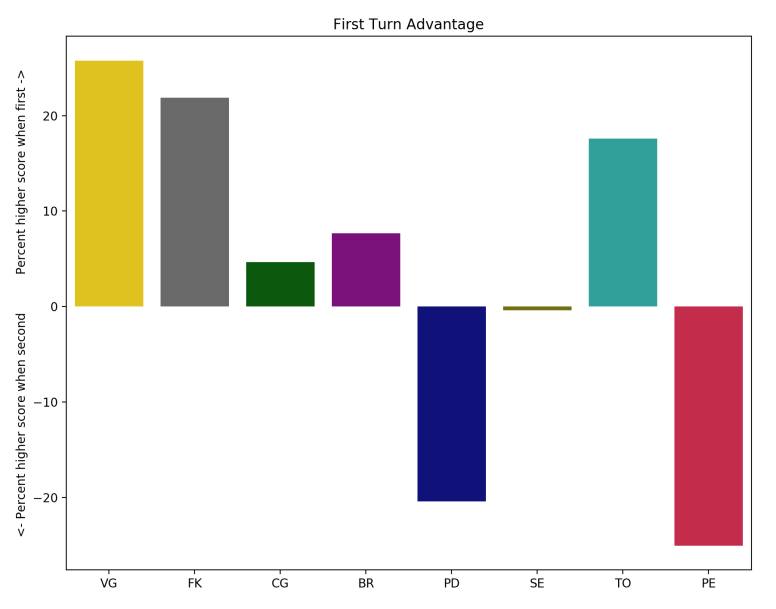
Here we show the percent difference in score between going first and second for each faction (with negative indicating it’s stronger going second):

And here are the relative faction strengths if we display going 1st / 2nd separately

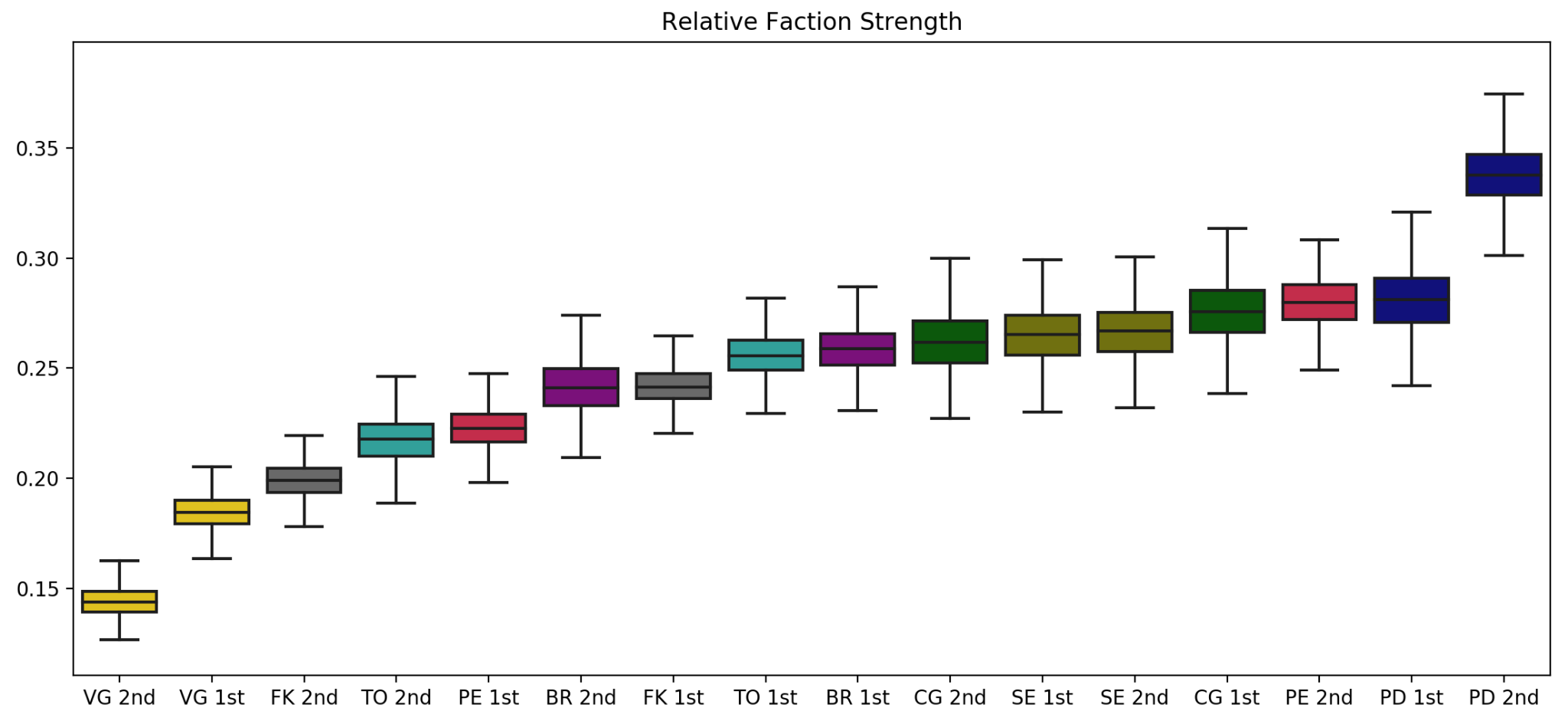
Now for a couple of takeaways. You may notice with the data so far Savanna Elves are just as strong going second as first. This is surprising since a number of strong players have argued that they want to go first as their starting setup is much better when given the first turn. My explanation is twofold: They may have a great setup when playing first, but their cards and strategies benefit from playing a slow defensive game. In the end these may balance out. Two, this could easily be an artifact of the data we have. It may be a factor of the matchups it’s had in the league, or just that pesky margin or error thing. Also, if you look purely at the overall 1st/2nd win rates (without all the math), SE is also pretty close to even when going 1st or 2nd.

It’s also interesting that PE are near the top when going second, but one of the worst when going first. No other faction has quite the spread.

And as a final note, I want to argue that your takeaway should be that the middle 6 of 8 factions are in fact quite balanced. Polar Dwarves are clearly the best, and Vanguards the worst, which is what the community has largely figured out. But for everything else, the difference really is within the margin of error and your experience with the faction you know will outweigh anything else.